内容:高速回転する切削工具では,遠心力による動的な振れを低減させるために,動バランスをとることが重要です.
しかしながら,動バランスをとるための構造がない切削工具も多いです.
ドリルで穴をあけて動バランスをとる場合,刃先のセットアップが変わるたびに追加工をしていると,いずれ限界がきます.
ねじ穴が空いていて,イモねじで動バランスをとる場合,イモねじを外せば再調整も可能ですが,既製品ではイモねじが取り出せない場合もあります.
そこで,自分で動バランス調整用の構造を追加工する場合を考えます.
このとき必要なのは,可能な穴加工やイモねじの挿入によって,どのくらいの動バランス修正が可能なのかを事前に評価しておくことです.
その評価のための計算が実施できます.
ここで想定しているのは,工具回転軸を中心として等間隔の位置に,ドリルで穴をあけたり,イモねじを取り付けることで,動バランス修正を行う場合です.
イモねじを取り付ける場合は,まずネジ穴をあけておいて,そこに質量を調整したイモねじを挿入します.
そのような設計において「どのくらいの動バランスまでなら修正できるのかどうか」を評価するには,想定している穴やイモねじ1個ずつで生じさせうる不釣り合いのベクトルの全組み合わせで実現しうる不釣り合いを計算すればいいです.
例えば,3つのねじ穴を120度間隔で空け,そこにイモねじを挿入する場合を考えます.
このとき,3つの不釣り合いベクトルがあることになり,その各ベクトルの大きさを\( U_{s} \)とします.
その全組み合わせで生じる不釣り合いの修正可能範囲は,1辺が\( U_{s} \)の正六角形になります.
\( U_{s} \)は,以下の式で得られます.
\( U_{s} = M_{s} \times R_{s} \)
\( U_{s} \):穴やイモねじによる1か所で修正できる最大不釣り合い
\( M_{s} \):穴やイモねじによる1か所で実現可能な最大可変質量
\( R_{s} \):穴やイモねじにおける可変質量の重心の半径位置
以下に示す図は,\( U_{s} = 1 \)として作図しています.
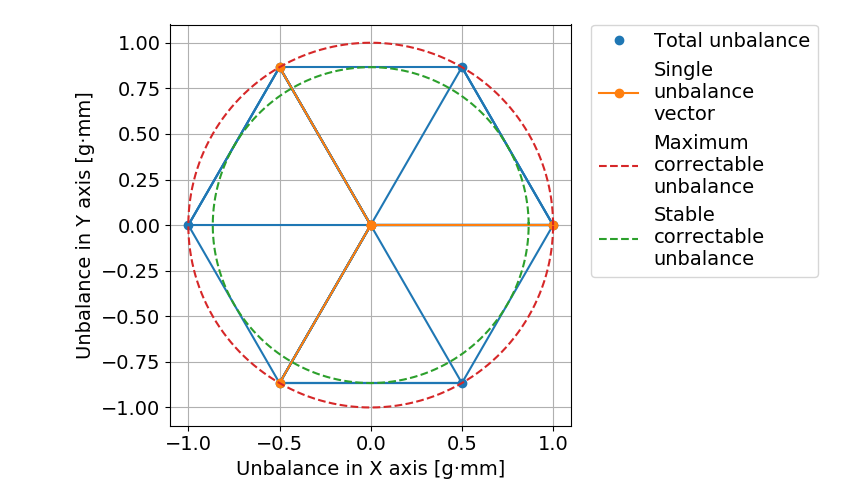
青線:最大不釣り合いベクトルベクトルの全組み合わせにより生じる軌跡
オレンジ線:穴やイモねじによる1か所での最大不釣り合いベクトル\( U_{s} \)(3つのねじ穴なので3方向)
赤点線:最外縁部の多角形の外接円
緑点線:最外縁部の多角形の内接円
他の穴数の場合は以下のようになります.
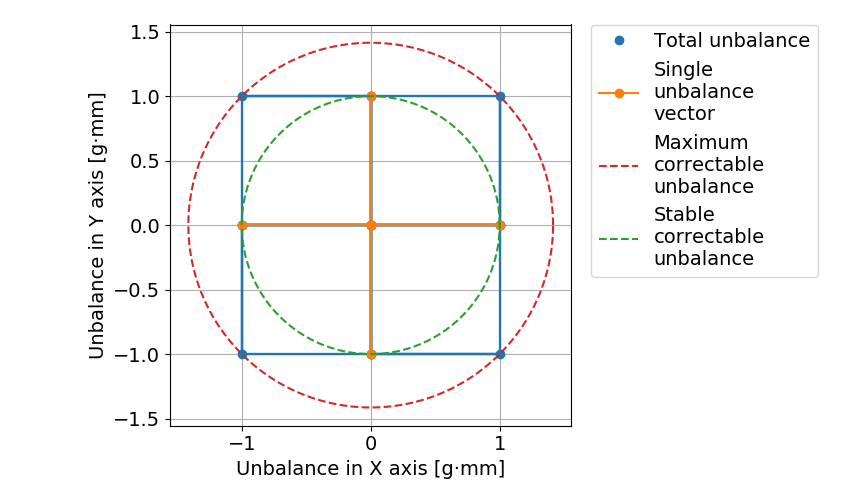
・4つのねじ穴を90度間隔であけてイモねじを入れる場合,1辺が\(2 \times U_{s} \)の正四角形.
・5つのねじ穴を72度間隔であけてイモねじを入れる場合,1辺が\( U_{s} \)の正10角形.
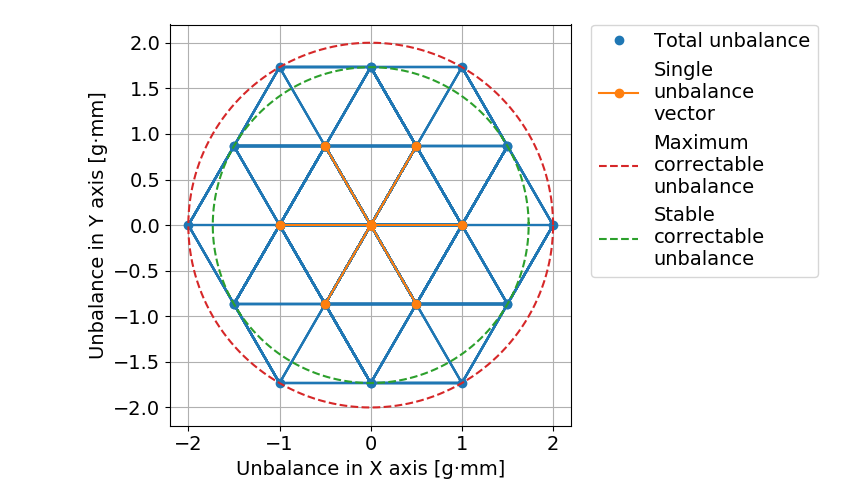
・6つのねじ穴を60度間隔であけてイモねじを入れる場合,1辺が\(2 \times U_{s} \)の正六角形.
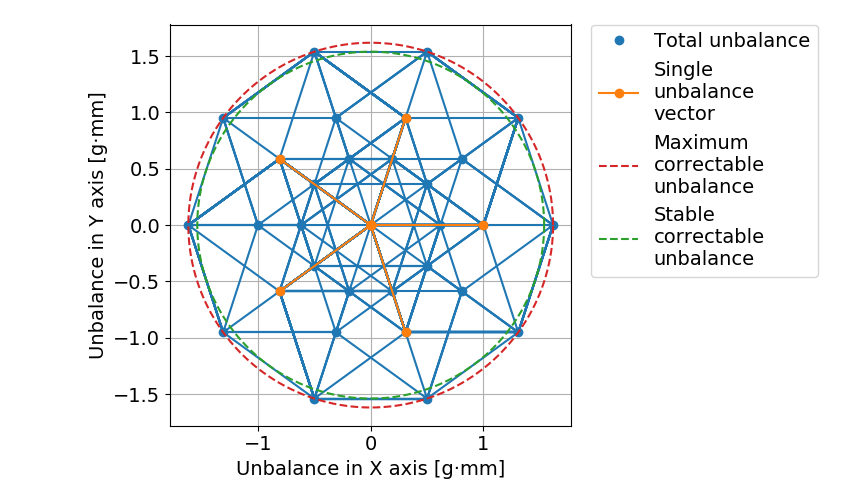
・7つのねじ穴を51.42度間隔であけてイモねじを入れる場合,1辺が\( U_{s} \)の正14角形.
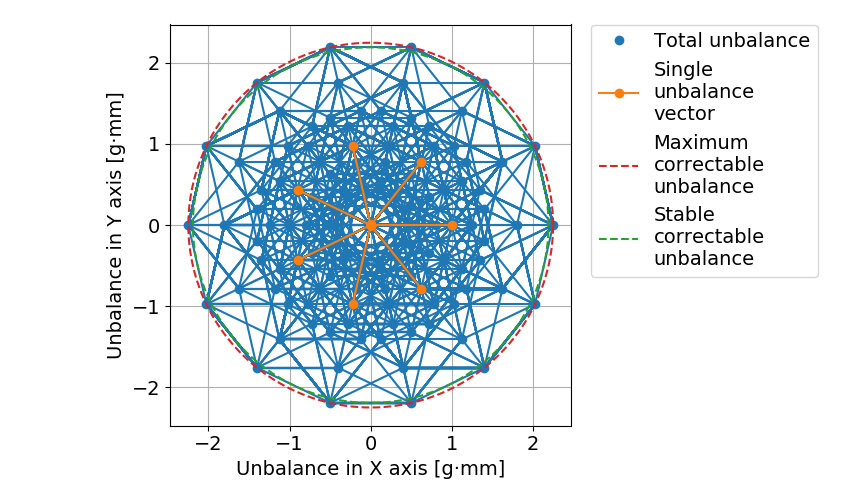
・8つのねじ穴を45度間隔であけてイモねじを入れる場合,1辺が\(2 \times U_{s} \)の正八角形.
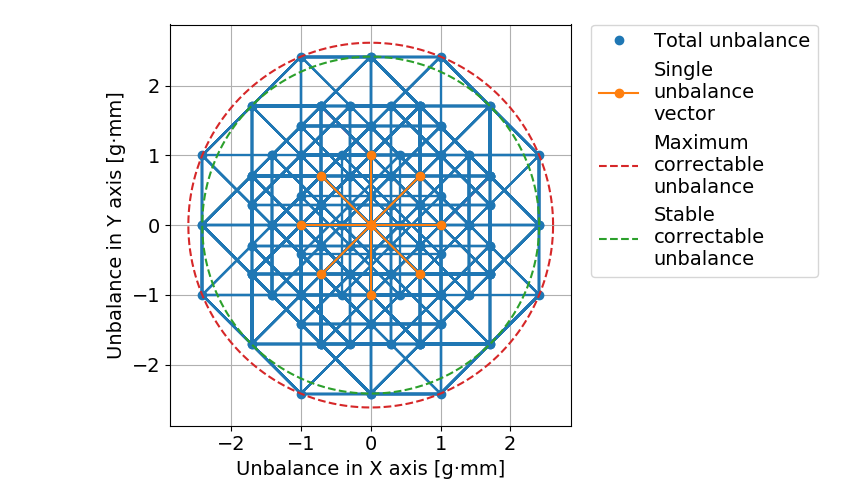
これらをまとめると,修正可能範囲の形状は以下のようになります.
・穴数が偶数,ここでは\(2 \times n \)のとき,1辺が\(2 \times U_{s} \)の正「\(2 \times n \)」角形.
・穴数が奇数,ここでは\(2 \times n -1 \)のとき,1辺が\( U_{s} \)の正「\(2 \times (2 \times n -1) \)」角形.
ただし,\( n \)は自然数とし,穴数は3個以上とします.
多角形なので,修正可能な不釣り合いの最大値は,多角形の外接円の半径になります.
これを最大修正可能不釣り合いと定義しています.
この最大値は,頂点までの距離なので,方向によっては,実現できない場合があります.
方向性を考慮せずに不釣り合い修正を行う場合は,その多角形の内接円の半径を修正可能範囲として考えてやればよいです.
これを安定修正可能な不釣り合いと定義しています.
これら2つの数値は,以下の数式で得られます.
・穴数が\(2 \times n \)のとき,
\( U_{max} = \cfrac{ U_{s} }{\sin( \cfrac{ 2\pi }{2 \times 2n})} = \cfrac{ U_{s} }{\sin( \cfrac{ \pi }{2n})} \)
\( U_{stable} = \cfrac{ U_{s} }{\tan( \cfrac{ 2\pi }{2 \times 2n})} = \cfrac{ U_{s} }{\tan( \cfrac{ \pi }{ 2n})} \)
・穴数が\(2 \times n -1 \)のとき,
\( U_{max} = \cfrac{ U_{s} }{2 \times \sin( \cfrac{ 2\pi }{2 \times 2 \times (2n-1)})} = \cfrac{ U_{s} }{2 \times \sin( \cfrac{ \pi }{ 2 \times (2n-1)})} \)
\( U_{stable} = \cfrac{ U_{s} }{2 \times \tan( \cfrac{ 2\pi }{2 \times 2 \times (2n-1)})} = \cfrac{ U_{s} }{2 \times \tan( \cfrac{ \pi }{ 2 \times (2n-1)})} \)
\( U_{max} \):最大修正可能不釣り合い
\( U_{stable} \):安定修正可能不釣り合い